Avec "pinwheel tiling" vous saurez vite de quoi il s'agit. Avec "pavage en moulin à vent", la traduction, ce sera bien plus réduit. Nous parlerons donc de PinWheel, plus simplement de PW et pour rester discret de pavage PW. Dessiner des pavages PW est un exercice amusant, totalement accessible parce qu'il suffit de deux objets très simples. Le premier est une feuille de papier, grande pour les personnes patientes par exemple 65 cm x 50 cm (cadre rouge) avec une fenêtre pour faire joli par exemple 40cm x 53 cm, petite si c'est juste pour voir.

Le second est un principe de découpage d'un triangle particulier :

Un triangle PW est un triangle rectangle dont le grand côté de l'angle droit a une longueur double de celle du petit côté de l'angle droit. Il se décompose très simplement en cinq triangles PW plus petits, lesquels pour la même raison se décomposeront en cinq nouveaux triangles PW encore plus petits ...
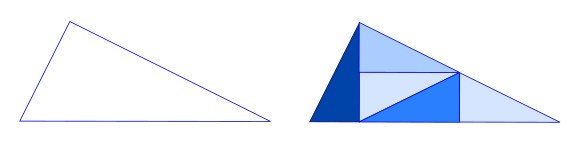
D'où le pavage PinWheel de la feuille : On peut toujours mettre la feuille dans un triangle PW au moins en pensée et commencer le découpage :

Le principe est simple, on peut écrire un programme qui fera des figures parfaitement exactes :

Il s'agit ici d'y mettre la main. Cette procédure est évidemment mathématique : Elle génère une figure aux propriétés curieuses. C'est un pavage acyclique, on n'y retrouve jamais une figure qui revient régulièrement. Les triangles sont orientés dans toutes les directions sans direction particulière, cette petite règle simple génère des variations cahotiques à l'infini. L'invention est de Charles Radin (The pinwhccl tilings of
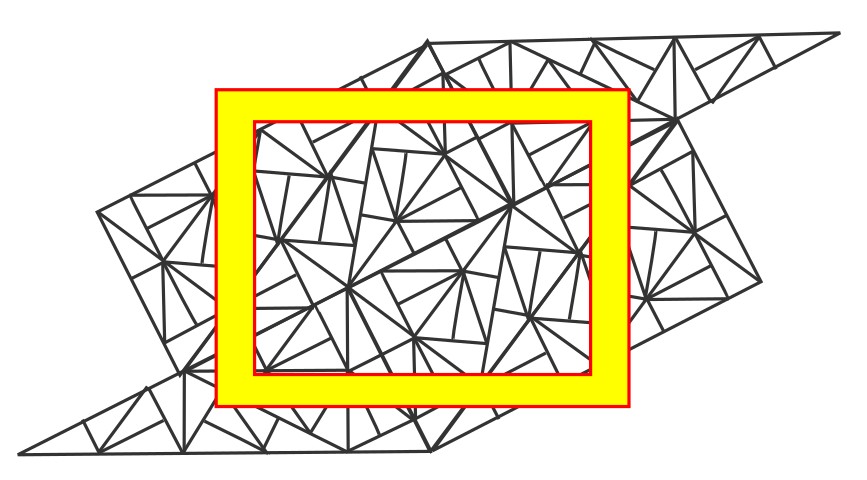
the plane Annals of Mathematics, 139 (1994), 661-702). L'approche pratique est hésitante au début car on ne peut tracer le premier triangle bien trop grand.

Puis la mécanique s'installe :

Un dernier niveau et ça devient fastidieux :

On remarquera que chaque niveau est coloré à l'aide de trois couleurs. Ceci n'est pas contenu dans la procédure de base, loin de là. C'est un théorème récent qui dit :

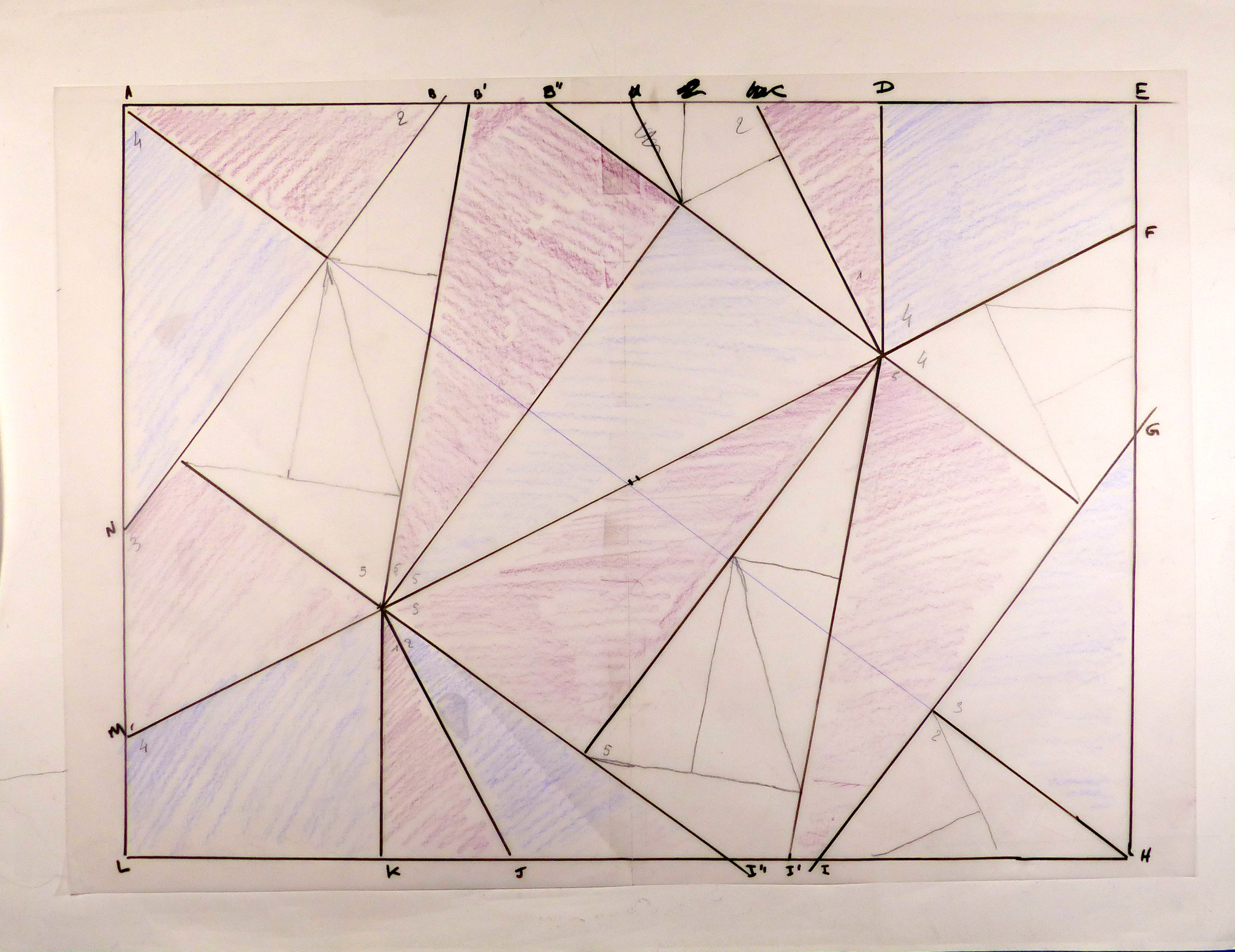
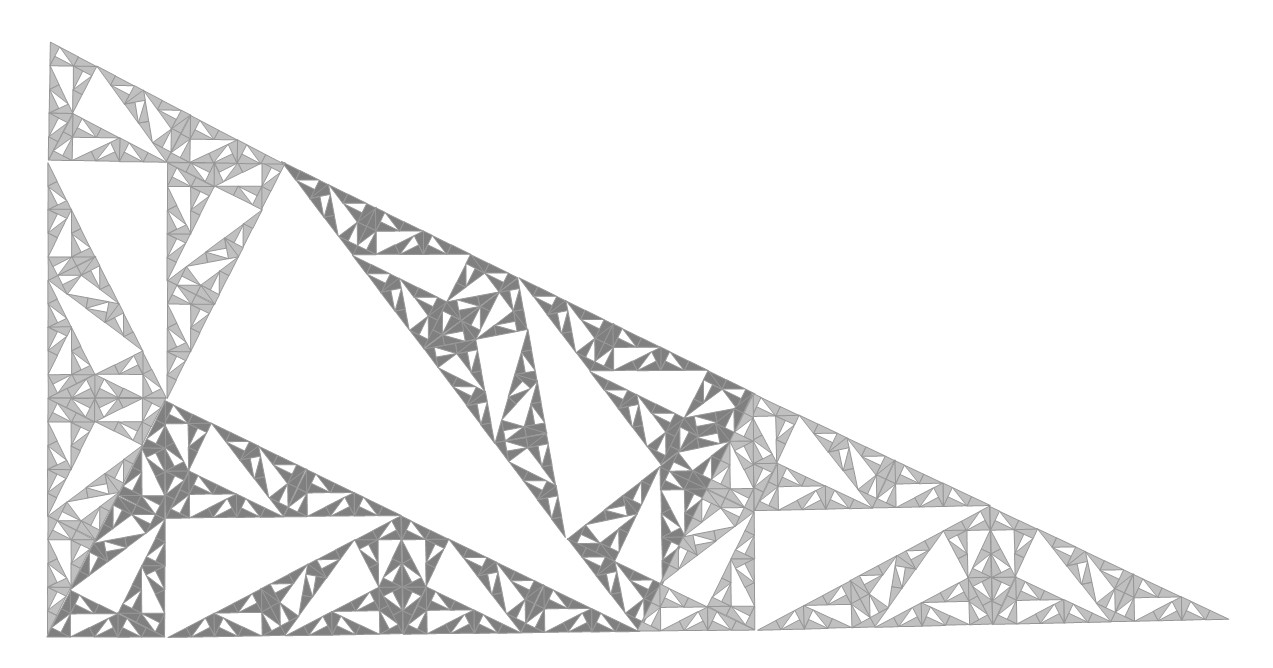
Theorem 6.9.The minimal number of colours needed to colour the faces of the pinwheel tiling is 3.

Cela veut dire que trois couleurs suffisent pour que chaque triangle d'un niveau donné ait une couleur différente de tout autre avec lequel il y a une frontière commune. Trois couleurs suffisent, c'est un résultat spectaculaire. Et trouver comment faire est un vilain problème. Tout est résolu dans l'article Colourings of aperiodic tilings de Molly Evans, Dylan Gawlak, Christopher Ramsey, Nicolae Strungaru and Ryan Trang 2022 (https://doi.org/10.48550/arXiv.2209.06364)
Graphiquement on arrive à un drôle d'endroit où forme et couleur ont deux statuts différents, relèvent de deux questions différentes. La forme est fractale, la couleur est définie à une échelle. En effet le pavage peut être vu comme un découpage ou un assemblage ou les deux et on peut mélanger les échelles pour rendre compte de la procédure :

source

Au contraire, les trois couleurs suffisantes n'ont de sens qu'à une échelle données et aucun lien ne lie un coloriage à l'autre. Il peut sembler intéressant d'explorer l'intervalle laissé libre.